The Euler-Mascheroni constant

We saw before that the natural logarithm function had a McLaurin expansion,

ln (1+x) = x - x^2/2 + x^3/3 - x^4/4 +..... ---------------------(2)

which was valid absolutely within the unit circle. Outside this we will begin seeing a discrepancy between the sum of the series on the right hand side of (2) and ln (1+x). Using Taylor's theorem the error term can actually be calculated and the series treated as an approximation to the function. Then, as x grows large without bound, what becomes of this discrepancy?

We define,

 = lim_{n->infinity}  1 + 1/2 + 1/3 + .... + 1/n   - ln n

 

We immdiately see by the bounds imposed by the Taylor series (2) that  

exists.

See http://planetmath.org/?op=getobj&from=objects&id=8771

Since 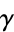 exists we in turn have another way to prove that the harmonic series diverges given the natural logarithm does!