To sum or not to sum...

Of course, the excursion taken in studying the harmonic series promises to be most fruitful in understanding how summation fits into the broader mathematical programme.

We have already seen that a traditional idea of summation where the sum of some terms (a_k) is,

S = a_0 + a_1 + a_2 + a_3 + ..... + a_(n-1) + a_n

and that taking the limit of S as n-> infinity gives us a way to sum the infinite series. This is essentially the idea behind the Cauchy sense of sum. The summation we are so familiar with that it becomes second nature to think of it synonymous with the very concept of summation.

If we were to stop here then we'll have succeeded at the original goal- in that we have now defined to an acceptable precision what we mean by summation. However, this playing field in particular, perhaps more than any other in contemporary mathematics (even counting non-Euclidean geometries) opens us doors to much more exotic possibilities.

It became plain to see that just as we have no general formula that can offer a closed form for each and every sum (even in the regular sense), there is no obligation presented that should limit us in extending the notion of a sum in different directions.

As a case in point, let us define the Ramanujan sum of a sequence (a_n) as,

S := sum_{n = 1}^{infinity} a_n  - integral_{1}^{infinity} a(t) dt   , (R)

Whereby we immediately have,

H := 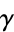 , (R)

by just a matter of definition!

Most interesting is that the Laurent expansion of Riemann's zeta function,

Z(s) = sum_{n = 1}^{infinity} n^(-s)

(note that Z(1) = H)

gives,

Z(s) = 1/(1-s)  +  + ....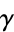

(where the terms represented by the trailing dots become zero as s->1, see http://en.wikipedia.org/wiki/Riemann_zeta_function#Laurent_series)

Thus, the Ramanujan summation procedure may be considered as removing the particular singularity that made the sum diverge while retaining a constant that is then given the function of the sum of the series.

Indeed, Ramanujan's idea was to treat the constant that arose from the Euler McLaurin summation formula as a representative quantity, or more loosely, the 'sum' of the series.

(See http://algo.inria.fr/seminars/sem01-02/delabaere2.pdf)